引入
前面我们说,算法效率要高,这里的高其实就是算法的执行时间短,时间段效率自然高,那么我们就需要了解,如何判断一个算法的执行效率,也就是执行时间快不快。
事后统计法
我们知道,跑马拉松,选手快不快,是根据到达终点的时间来决定的。算法也一样,我们根据跑完一遍的时间来计算算法的效率。也就是事后统计法。
事后统计法:通过设计好的测试程序和数据,利用计算机计时器对不同的算法编程的程序的运行时间进行比较。从而确定算法的效率高低。
事后统计法的缺陷
这种事后统计法是需要测试程序和数据的….
准备测试程序和数据太费功夫了….
因为测试数据和程序要跟算法一对一匹配。
测试失败…不就凉了…
特别是:不同的测试环境,测试的结果
差别非常大。
事前分析估算法
因为事后统计法太不准确了,所以在计算机程序编写前,依据统计方法对算法进行估算。那么用啥统计方法呢?
根据总结,发现了高级语言在计算机上运行所消耗的时间主要有以下因素:
- 算法采用的策略和方案
- 编译产生的代码质量(也就是编译器的优劣)
- 问题的输入规模
- 机器执行指令的速度(CPU 和内存的速度)
如果,我们抛开计算机硬件和软件的因素,其实最重要的就是输入规模和算法的好坏。(输入规模就是输入量的多少)
几个例子
我们既然知道,输入规模和算法是判断一个算法效率的重要指标,那么我们就举几个例子,在不同的算法和不同的输入规模下,看看会发生生么?
发现问题
还是求 1+2+3+....+99+100 的例子
累加算法
1 | int i,sum=0,n=100; //执行了1次 |
高斯算法
1 | int i,sum=0,n=100; //执行了1次 |
好,我们现在使用了两种算法。
第一种算法执行了
1+(n+1)+n=2n+2 次
第二种算法执行了
1+1=2 次
如果我们把循环看做一个整体,忽略头尾判断,那么两个算法就是 n 和 1 的差别。
等等… 2n+2 和 2 怎么会只有 1 和 n 的差别?别闹…
解决问题
我们研究算法的复杂度,研究侧重的是算法随着输入规模扩大的增长量的一个抽象。并不是要严格的计算究竟执行了多少次,如果要严格计算,这就没完了~
- 抽象:我们不关心用什么语言、不关心计算机的速度,只关心它所实现的算法,这就是抽象!
也就是说,我们不计算:
- 循环的增量和判断
- 变量声明
- 打印结果
- 等等
注意
我们要把程序从程序语言中剥离出来,只看算法!
我们在分析一个算法时,主要是把操作的数量和输入模式关联起来!
例一
两个算法
- 算法 A:执行2n+3次操作,n 看做循环,2个循环,3个赋值运算。
- 算法 B:执行3n+1次操作,n 看做循环,3个循环,1个赋值运算。
那么上面的两种算法,哪一种效率更高呢?我们先看看图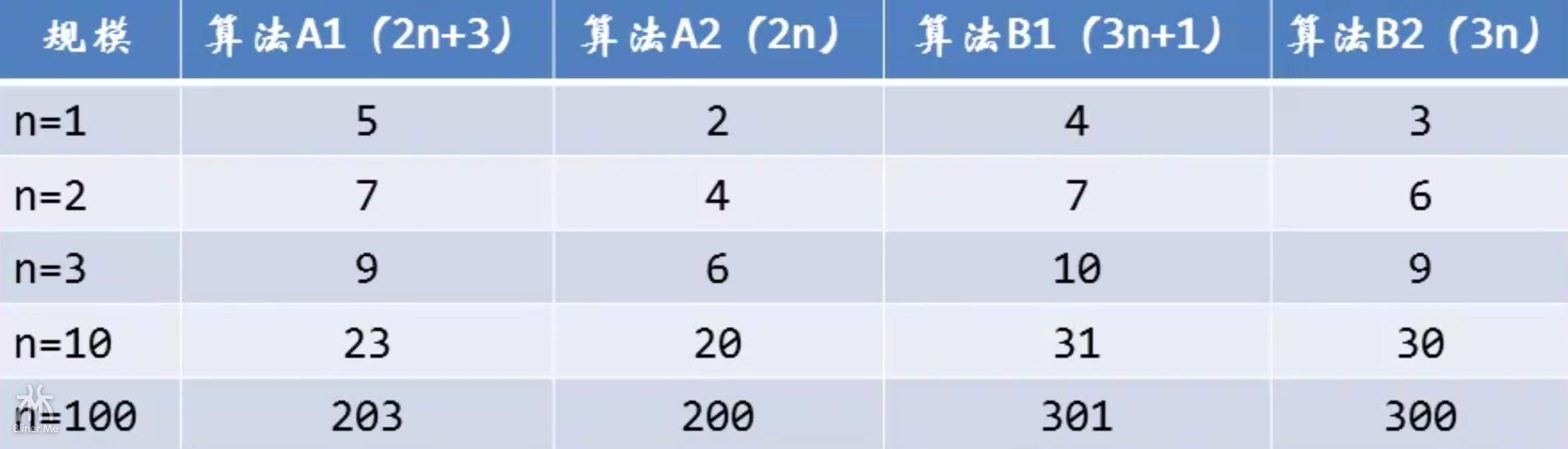
(图片来自鱼c工作室)
我们看到
n=1 时,A1 算法要5次算完,A2 算法要4次,A2 好于 A1。
n=2 时,A1 算法要7次算完,A2 算法要7次,A2 等于 A1。
n=3 时,A1 算法要9次算完,A2 算法要10次,A2 劣于 A1。
n=100时,A1 算法要203次算完,A2 算法要301次,A2 劣于 A1。
总得来说,在 n=2之前,A2 好于 A1,之后 A1 好于 A2
我们上面算的都是输入一定时,算法要运行的次数。
我们看一下渐进图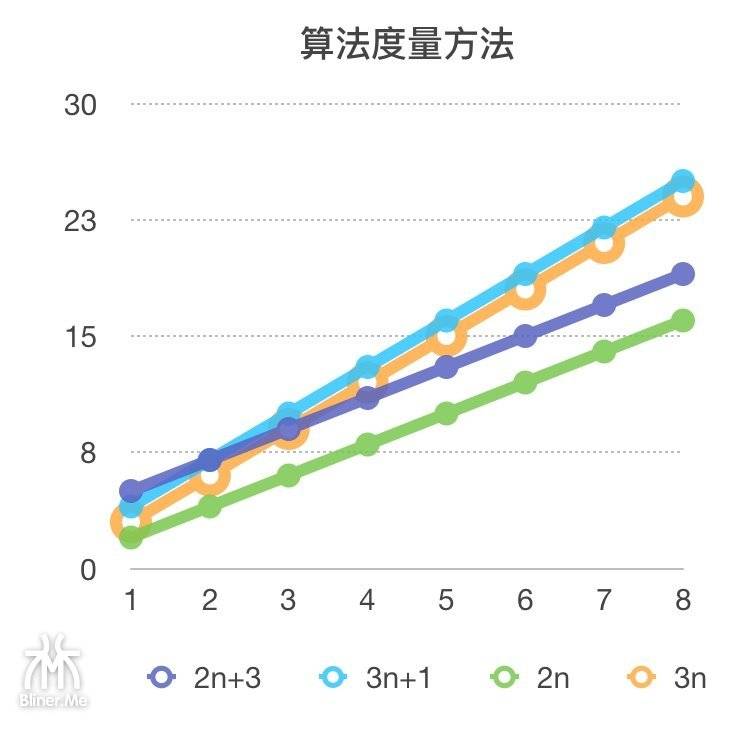
我们看到 2n+3 和 3n+1 在2处交汇,并交换了位置,所以:
如果对于函数 f(n) 和 g(n) ,如果存在一个整数N,使得所有的 n>N,f(n)>g(n),那么我们就说 f(n) 的增长渐进快于 g(n)。
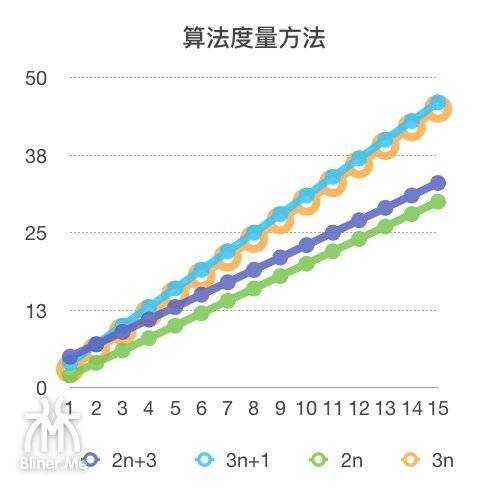
我们将范围拉大,仔细看,2n+3 、2n 和 3n+1 、 3n,后面 +3 还是 +1 其实对最后的算法变化影响不大,因为 2n+3 和 2n 的曲线几乎重合了, 3n+1 和 3n 也是如此。所以:
概念:在计算时,可以
忽略这些加法常数,即算法中如果加上了这个常数,我们可以不把它们考虑在内,因为它们在输入规模变大时,没有影响。
例二
再来一个例子,两个算法
- 算法 C:执行4n+8次操作,n 看做循环,4个循环,8个赋值运算。
- 算法 D:执行$2n^{2}+1$次操作,n 看做循环,2个嵌套循环,1个赋值运算。
我们还是看看图
我们看到
n=1 时,C1 算法要12次算完,C2 算法要3次,C2 好于 C1。
n=3 时,C1 算法要20次算完,C2 算法要19次,C2 几乎等于 C1。
n=6 时,C1 算法要32次算完,C2 算法要73次,C2 劣于 C1。
我们再看一下渐进图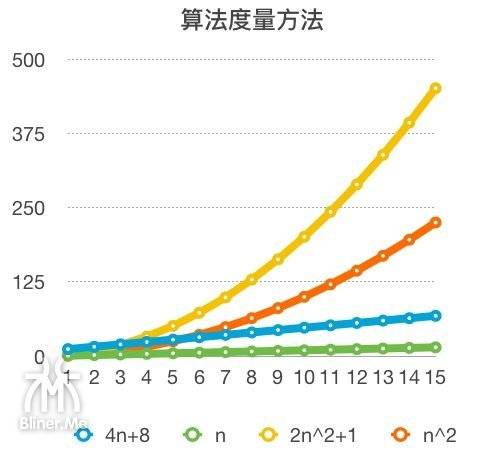
我们前面说,4n 和 4n+8 的+8其实可以忽略了,我们看,果然曲线的变化趋势上差别不大。
我们再看,$2n^{2}+1$ 和 $n^{2}$ 一个有相乘的常数2,一个没有,但是趋势跟 4n 和 4n+8 比$2n^{2}+1$ 和 $n^{2}$ 还是非常接近的,所以$2n^{2}+1$ 和 $n^{2}$ 中的相乘的常数2,也可以忽略不计。
概念:算法运算次数的统计中,与最高次项相乘的常数并不重要,也可以忽略。
例三
接着来一个例子,两个算法
- 算法 E:执行$2n^{2}+3n+1$ 次操作,n 看做循环,2个嵌套循环,3个循环,1个赋值运算。
- 算法 F:执行$2n^{3}+3n+1$ 次操作,n 看做循环,2个三嵌套循环,3个循环,1个赋值运算。
我们还是看图

我们看到
n=1 时,E1 算法要1次算完,F2 算法要1次,F2 好于 E1。
n=2 时,E1 算法要15次算完,F2 算法要23次,F2 劣于 E1。
n>1 时,E1 和 F2 的差距越来越大,E1 越来越好,F2越来越差。

我们再看,$2n^{2}+3n+1$ 和 $2n^{3}+3n+1$ 虽然只有 n 的指数不同,但是差距确是,非常大的,这一点从 $n^{3}$ 也可以看出。
概念:最高次项的指数大的,函数随着 n 的增长,结果也会增长的特别快。所以 n 的指数大不大才是最关键的。
例四
最后看一个例子,三个算法
- 算法 G:执行$2n^{2}$ 次操作,n 看做循环,2个嵌套循环。
- 算法 H:执行$3n+1$ 次操作,n 看做循环,3个循环,1个赋值运算。
- 算法 I:执行$2n^{2}+3n+1$ 次操作,n 看做循环,2个嵌套循环,3个循环,1个赋值运算。
惯例看图
渐近线图
缩小图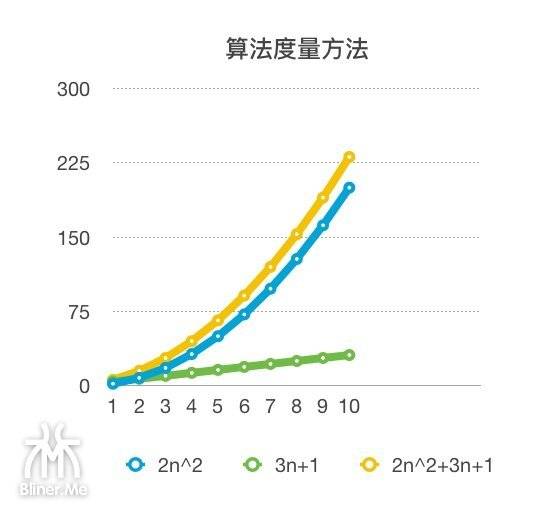
我们发现当数值变的非常大的时候3n+1这种 n 上不带指数的已经没有办法和带指数的$2n^2$相比了。
解决问题
综合上面四个例子,我们知道:
- 加一个常数我们可以忽略
- 一个乘数乘数可以忽略
- n 上的阶数最重要
函数的渐进增长:判断一个算法的效率时,函数中的常数和其它次要项常常可以忽略,而更应该关注主项(最高项)的阶数。
注意
在判断一个算法好不好的时候,只通过少量数据是没办法准确判断。
尾巴
这是我的个人学习笔记,主要是应付考研复习使用,充斥着一些吐槽和个人观点,并不严谨,欢迎大家参考、指正。


