引入
我们上节课我们讲了三条性质,从层数、层节点数、深度、总结点数、以及度的概念了解了二叉树的一些有趣的性质,今天我们继续看看,二叉树还有什么有趣的特性。
从节点数判断深度,从深度判断节点数
预习一下取整符号:
- $\left \lfloor 这是向下取整符号 \right \rfloor$
- $\left \lfloor 2.4 \right \rfloor=2$ 向下取整到2
- $\left \lceil 2.4 \right \rceil=3$ 向上取整到3
具有 n 个结点的完全二叉树的深度 K 为$\left \lfloor \log_{2}n \right \rfloor+1$
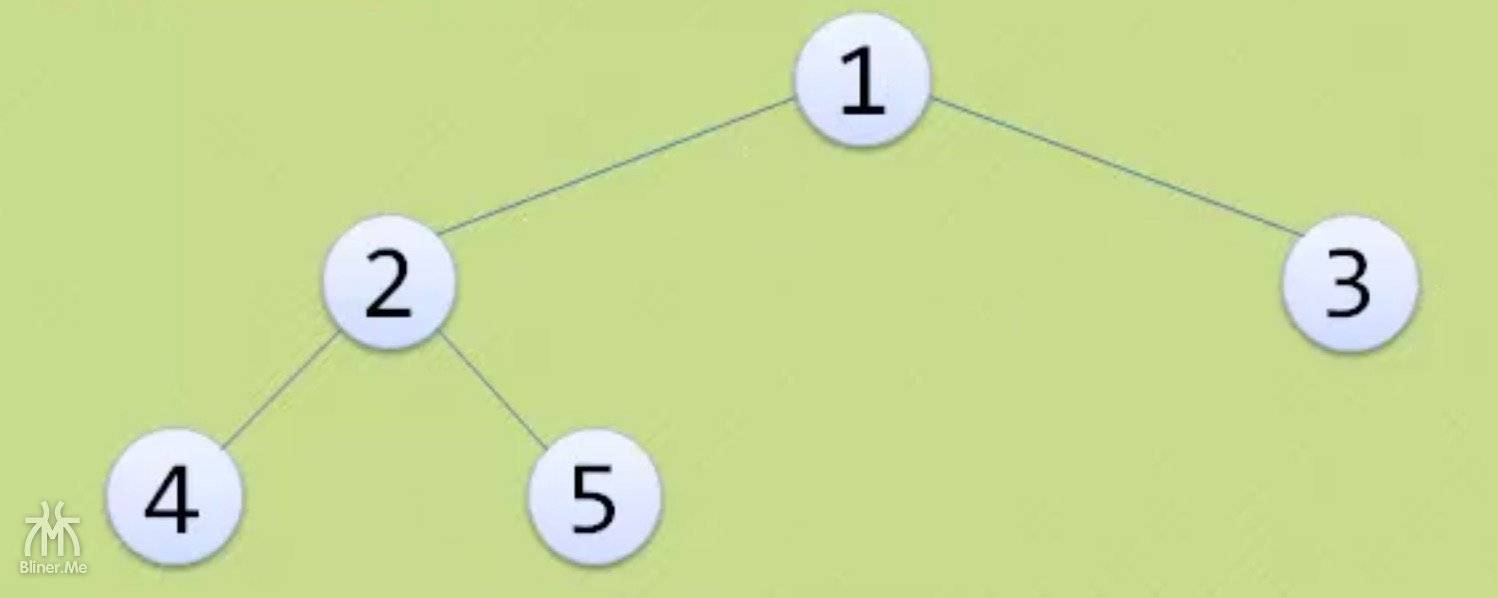
- n 表示完全二叉数的结点数,上面的图中 n=5
- 上图的完全二叉树的深度为:$\left \lfloor \log_{2}5 \right \rfloor+1$
- $2^n=5$然后 n 再加 1。
- $n \approx 2.3$,再加上向下取整$\left \lfloor 2.3 \right \rfloor=2$
- 得到$2+1=3$,这棵完全二叉树有 3 层
我们再看看满二叉树如何通过结点数判断深度
- 之前我们直到深度为 k 的满二叉树的节点数为$n=2^{k}-1$个。
- 我们倒推一下$n=2^{k}-1$,得到满二叉树的深度为 $k=\log_2(n+1)$。
还记得完全二叉树的叶子吗?只会出现在最下面两层,所以我们可以推出
- 完全二叉树的倒数第二层一定是满二叉树,就像上面的图。
- 如果完全二叉树的倒数第二层没有满,就开始最后一层的内容,肯定就不是完全二叉树了,所以
完全二叉树的倒数第二层一定是满二叉树,完全二叉树倒数第二层的满二叉树的结点数为$n=2^{(k-1)}-1$。上图的计算就是- $n=2^{3-1}-1=3$,所以倒数第二层的回推总点数为 3
综上,我们知道了
完全二叉树倒数第二层满二叉树的最大节点数,$n=2^{(k-1)}-1$完全二叉树深度为 k 的最大结点树为$n=2^{k}-1$- 所以,
完全二叉树结点 n 的取值范围是:$2^{(k-1)}-1 < n \leq 2^{k}-1$ - 所以,$2^{(k-1)} < n \leq 2^{k}$
- 左右取对数,$k-1 \leq log_2n < k$
- k 也要取整,具有 n 个结点的
完全二叉树的深度 K 为$\left \lfloor \log_{2}n \right \rfloor+1$
按层序编号的完全二叉树的一些性质
如果有一个 n 个结点的完全二叉树
- 深度为 $\left \lfloor \log_{2}n \right \rfloor+1$ 的结点按层序编号
- 对于任一结点 i ($1 \leq i \leq n$)
- 对于上面的这棵完全二叉树,都有一下性质成立

结点 i 的序号
- 如果 i=1 , 则结点 i 是二叉树的根,根无双亲。
- 如果 i>1,则双亲是结点$\left \lfloor\frac{i}{2} \right \rfloor $
- 例如 i=4,双亲结点是$\left \lfloor\frac{4}{2} \right \rfloor =2$
- 例如 i=3,双亲结点是$\left \lfloor\frac{3}{2} \right \rfloor =\left \lfloor 1.5 \right \rfloor=1$
- 如果2i>n,并且结点 i 为叶子结点,则结点 i 没有左孩子
- 例如i=3,$ 2 \times 3=6 > 5$,结点 3 并有左孩子
- 结点 i 的左孩子是 2i
- 例如i=2,$ 2 \times 2=4 $,结点 2 左孩子为4
- 如果2i+1>n,则结点 i 没有右孩子
- 例如i=3,$ 2 \times 3=6 $,结点 3 没有右孩子
- 结点 i 的右孩子都是 2i+1
尾巴
这是我的个人学习笔记,主要是应付考研复习使用,充斥着一些吐槽和个人观点,并不严谨,欢迎大家参考、指正。


