引入
上一节我们发现,树、森林和二叉树之间竟然有这么多有趣的关联,前根和后根遍历结果竟然都可以跟二叉树相同。二叉树竟然这么的独特,今天我们就来看看,如何打造一棵完美二叉树!
从一个问题出发
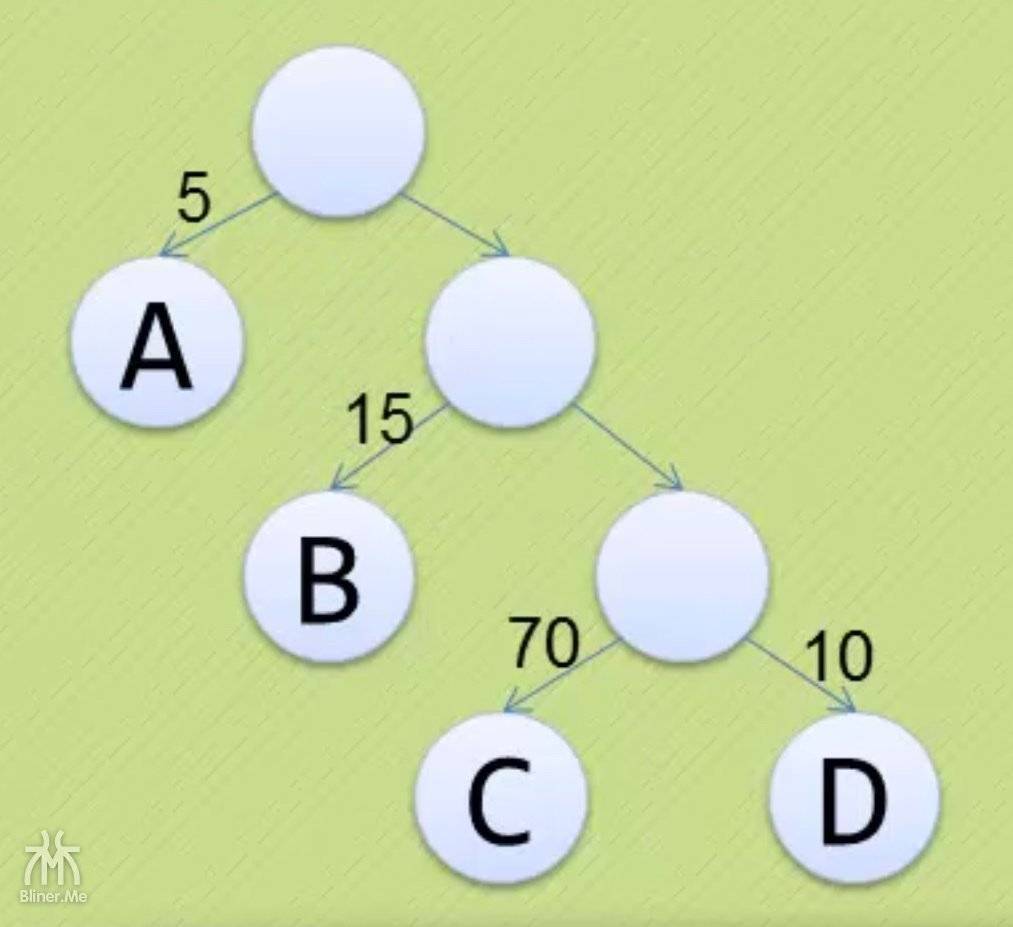
我们在使用二叉树的时候,会遇到类似这样的问题
- 这是一棵二叉树,结点连接线上的数字,是访问这个结点的概率
- 我们有5%的几率访问 A、15%访问 B、70%访问 C、10%访问 D
- 那么问题来了,既然绝大多数都是访问 C 的
- 那访问 C 必须要先判断是否是 A 或者 B,这样太麻烦了
要弄清楚这个问题,我先首先要弄清楚刚才哪些加了数字的结点是什么。
带权叶子结点

还是这张图,我们看到这棵二叉树有一点点不同
- 结点前有一个数值,我们把这种
结点间连线的相关书叫做权。 - 我们管这些叶子结点,叫做带权叶子结点。
- 数值越大,权重越大。
结点的路径长度

我们引申出一个新定义,结点的路径长度,我们来看一下
结点的路径长度
定义:根结点到叶子结点的路径上的连接数。
上图中,C 结点的路径长度为 3。
- 根到右子树,为1
- 右子树到右子树为,为2
- 右子树到右子树的左子树 C ,为3
树的路径长度
定义:根到每一个结点的路径长度之和。
上图中,我们来算一下
- 根到 A 是1
- 根到 B 是2
- 根到 C 是3
- 根到 D 是3
- 所以$1+2+3+3=9$
- 上面这棵
树的路径长度为9。
结点带权路径长度
结点的路径长度是根到结点,那么带上权呢?
定义:结点的路径长度与结点权值的乘积。
我们还是拿 C 结点举例
- C 结点的路径长度我们算过了,长度是 3
- 那么 C 结点的带权路径长度就是$3 \times 70=210$
- C 结点的带权路径长度为210
树的带权路径长度
定义:根到每一个结点的路径长度乘以权值的和。
上图中,我们来算一下
- 根到 A 是1,权值是5,$1 \times 5=5$
- 根到 B 是2,权值是15,$2 \times 15=30$
- 根到 C 是3,权值是70,$3 \times 70=210$
- 根到 D 是3,权值是10,$3 \times 10=30$
- 所以$5+30+210+30=275$
- 上面这棵
树的带权路径长度为275。
我们将树的带权路径长度称为 WPL(Weighted Path Length)
记住,WPL 就是树中所有叶子结点的带权路径长度之和。
最优二叉树
我们称 WPL 的值越小,构造出来的二叉树就约优秀,那么该如何构造出最优的二叉树呢?对了,最优二叉树我们也称为哈夫曼树!
初始化
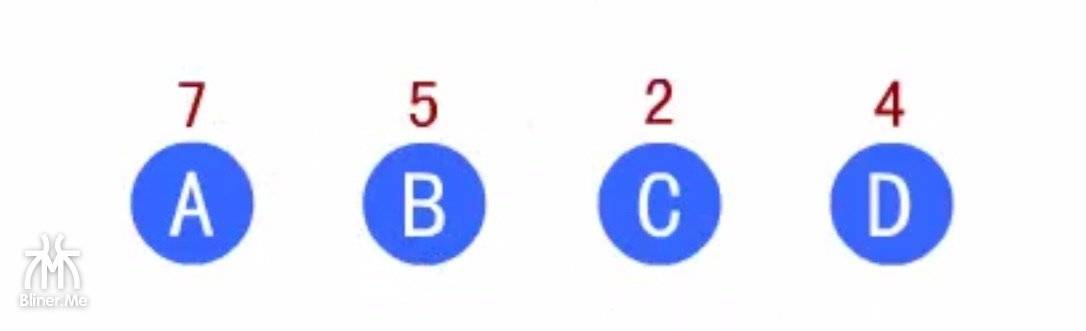
首先,我们在森林中选择两课根结点权值最小的树,上图所示
- 我们把 A B C D 看做四棵树组成的森林
- A B C D 就是四个根节点,四个根节点都有一个权值
- 我们把最小的两个提取出来,即 C 和 D
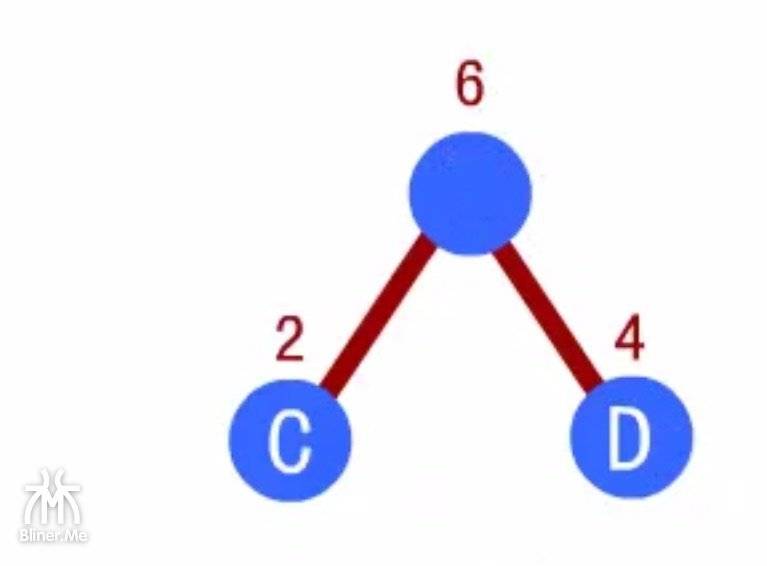
接着我们来操作上面的两个最小的结点
- 把两个结点中权值较小的放到左边,即 C 放到左边,作为左孩子
- 权值较大的结点放在右边,作为右子树
- 将左右子树的权值相加,得到6,作为左右子树的双亲结点,我们记作N1
继续添加
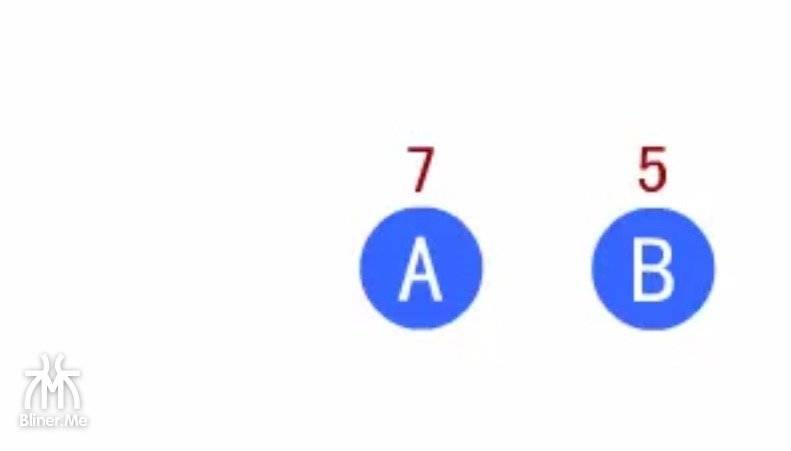
我们剩下的还有两个结点,A 和 B
- 上一步我们得到了一个 N1,权值是 C D 的和
- 此时我们从 A 和 B 中选择一个较小的结点 B,拿出来
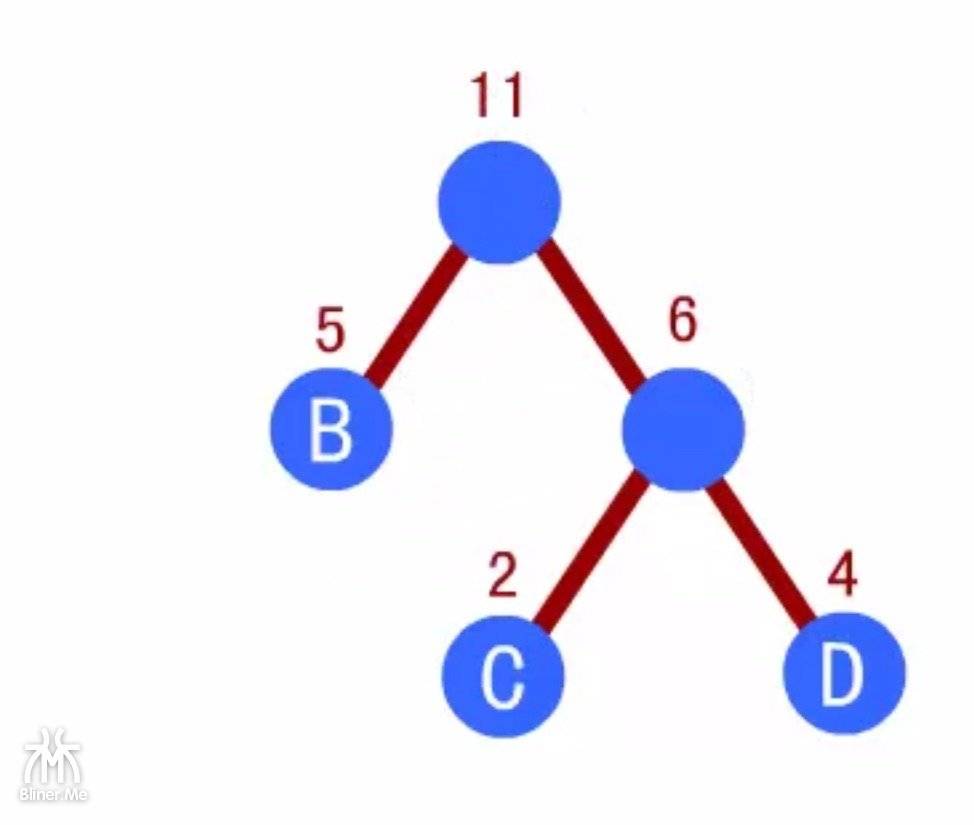
我们开始比较 B 和 N1
- 如果 B 比 N1 大,那就放右边作为右子树,反之作为左子树
- 因为 B 是5,N1是6,所以我们把 B 放在左边
- 同样的生成一个 N2,N2的权值是 N1和 B 的和,即5+6=11
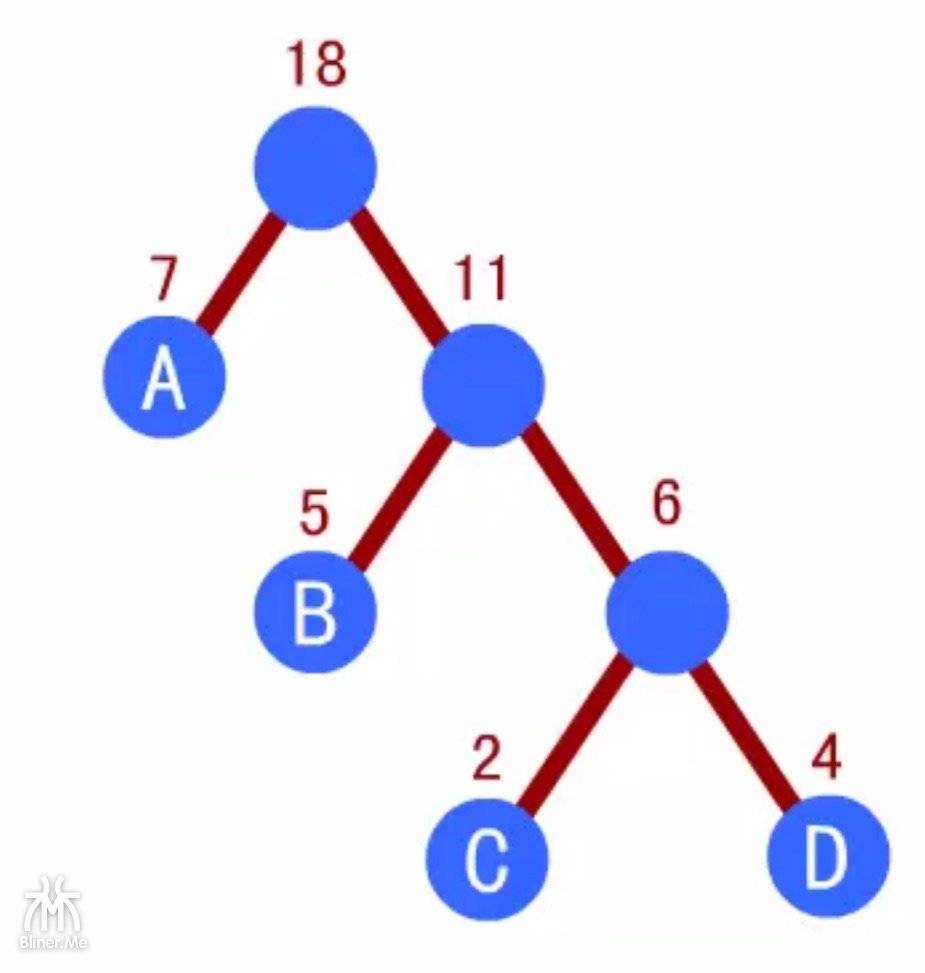
最后剩下的结点 A 相同,最后得到这棵哈夫曼树的根权值为18。
哈夫曼树构造完毕。
哈夫曼树的优点?
我们费劲儿构建的这棵哈夫曼树有什么厉害的地方呢?
- WPL 最小,WPL 还记得吧?就是树的带权路径
- 我们不可能构建出比哈夫曼树更好的排列方式
- 所以我们将哈夫曼树也成为
完美二叉树。
回到问题

还记得我们开头这个问题吗?既然访问节点的概率就是权值的话,我们用哈夫曼树的构建方式,将 A B C D 重新构建之后,就可以解决啦!
尾巴
这是我的个人学习笔记,主要是应付考研复习使用,充斥着一些吐槽和个人观点,并不严谨,欢迎大家参考、指正。


