引入
终于,我们迎来了新的数据结构,图结构。之前的线性表,主要是一对一的关系,一个元素和另一个元素的关系。树结构,主要层与层之间一对多的关系,即一个结点可以有 N 个子树,N 个子树也只对应一个双亲结点。那么大家也应该猜到了,图解决的是多对多的数据关系。
图的定义
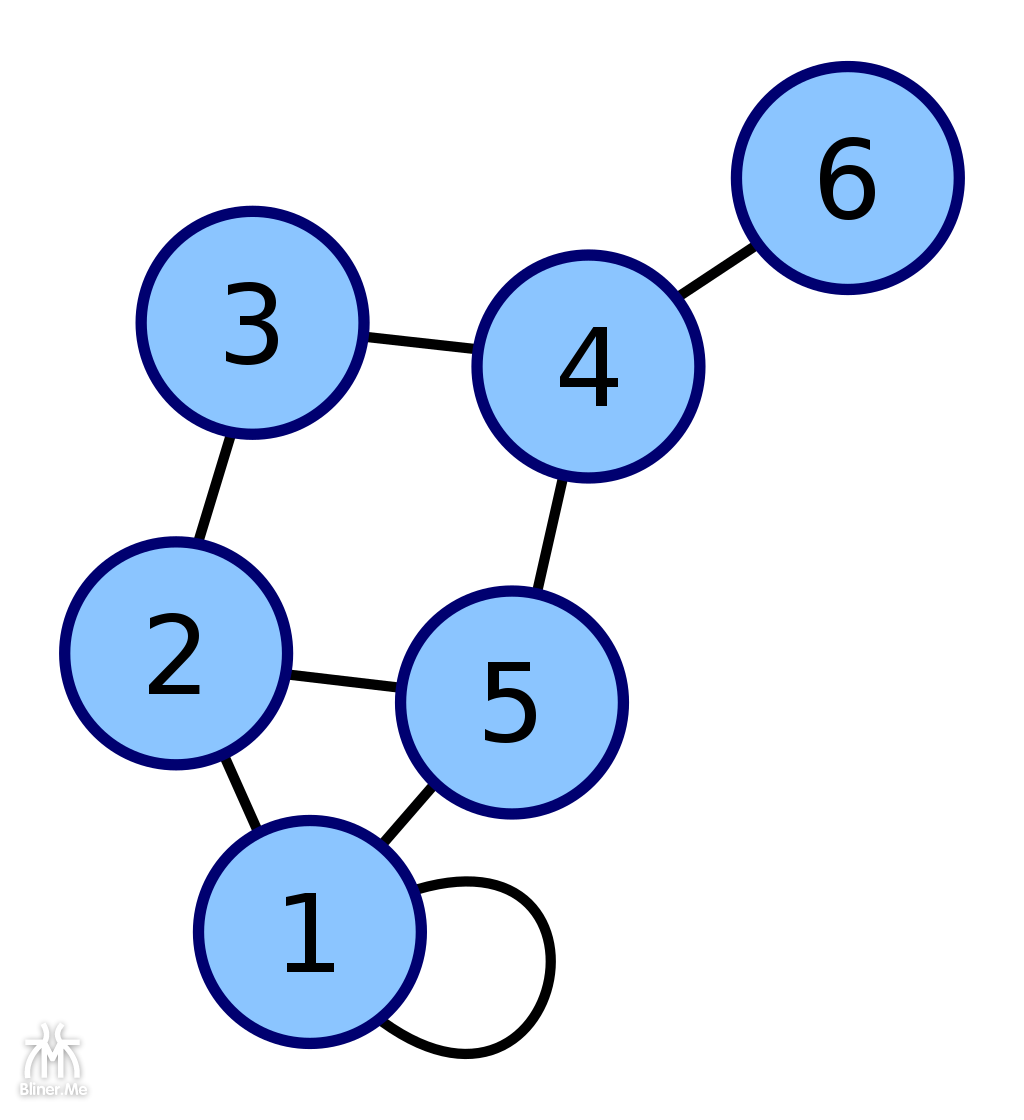
(顶点1有一个环的图结构)
图(Graph):是有顶点的又穷非空集合和顶点之间的边集合组成。
- 通常表示为G(V,E)
- G 是一个图
- V 是图 G 中顶点的集合
- E 是图 G 中边的集合。
对于上面的图
- 每一个圆圈表示图的一个顶点,顶点放在一起就是 V
- 连接顶点的连线称之为图的边,边放在一起就是 E
数据元素的称呼
我们回顾一下线性表和树的数据
- 线性表中我们把数据称之为元素
- 树中我们把数据称之为结点
- 图中我们把数据称之为顶点(Vertex)
没有数据元素
我们回顾一下线性表和树没有数据元素时
- 线性表可以没有数据元素,称为空表。
- 树中可以没有结点,称为空树。
- 图一般不为空,我们一般说
顶点集合 V 要有穷非空。
数据元素的关系
我们回顾一下线性表和树中数据元素之间的关系
- 线性表中的数据元素,一对一,我们说它们有线性关系。
- 树结构中的数据元素,一对多,我们说相邻两层的结点具有层次关系。
- 图结构中的数据元素,多对多,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以为空,即数据元素可以跟任何其他数据元素无关。
图的边
图中的各种特性和定义比较多,我们分开讲
无向边
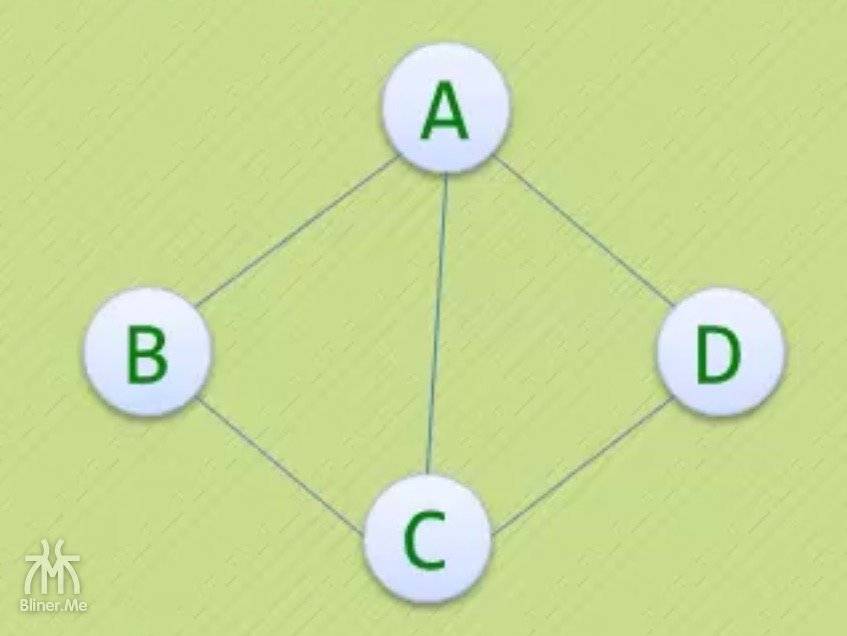
看着上面这张图,我们来说明一下
- 若顶点 Vi 到 Vj 之间的
边没有方向 - 则称这条边为
无向边(Edge) - 用无序偶(Vi,Vj) 来表示
- V 是顶点的集合哈,Vi 和 Vj 就是其中的两个顶点。别忘了。
知道了上面的概念之后,我们就可以说
- 上图G1是一个
无向图,如果 $G1=\left { V1 , E2\right }$ - 顶点的集合:$V1=\left{A,B,C,D\right}$
- 边的集合:$E1=\left{(A,B),(B,C),(C,D),(D,A),(A,C)\right}$
有向边
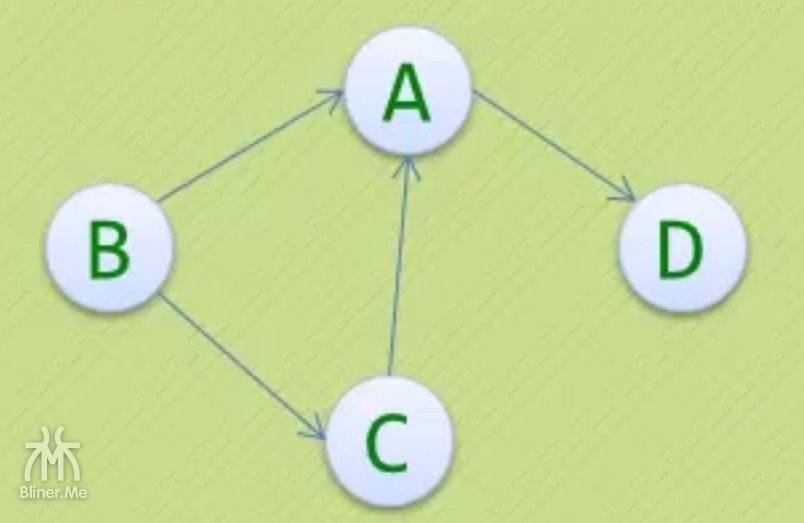
看着上面这张图,我们来说明一下
- 若顶点 Vi 到 Vj 之间的
边有方向 - 则称这条边为
有向边,也称为弧(Arc) - 用有序偶 < Vi , Vj > 表示,注意这里是尖括号
- Vi 称为弧尾,Vj 称为弧头。
- 因为是有向边,所有 Vi 和 Vj 顺序不能错,一定是尾巴指向头。
知道了上面的概念之后,我们就可以说
- 上图G2是一个
有向图,如果 $G2=\left { V2 , E2\right }$ - 顶点的集合:$ V1= \left{ A,B,C,D \right} $
- 边的集合:$E1=\left{(B,A),(B,C),(C,A),(A,D)\right}$
- 这里边的集合要注意顺序!!!
简单图
什么叫做简单图呢?在一个图结构中
- 若不存在顶点到其自身的边
- 同一条边不重复出现
- 满足以上两个条件的图,叫做简单图。
以下两个都不是简单图
| 同一条边出现两次 | A 不能指向自己 |
|---|---|
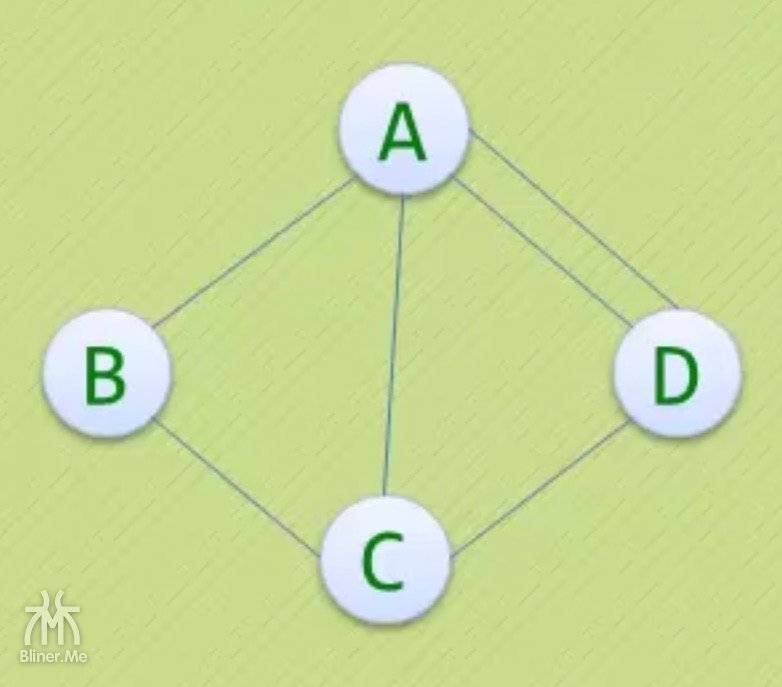 |
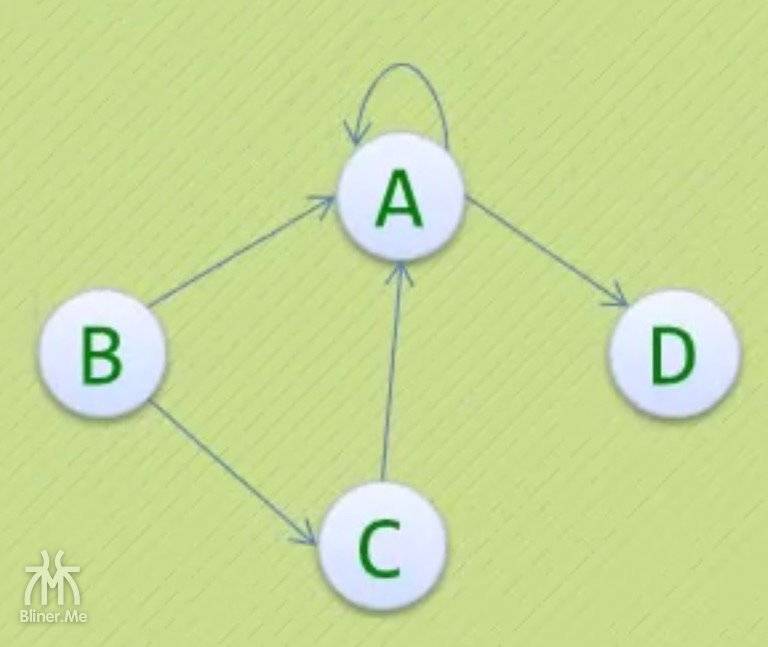 |
注意:我们目前讲的主要都是简单图,因为应用广泛。
特殊的图
根据图边、弧和顶点的不同情况,又分为以下几种常见图
无向完全图
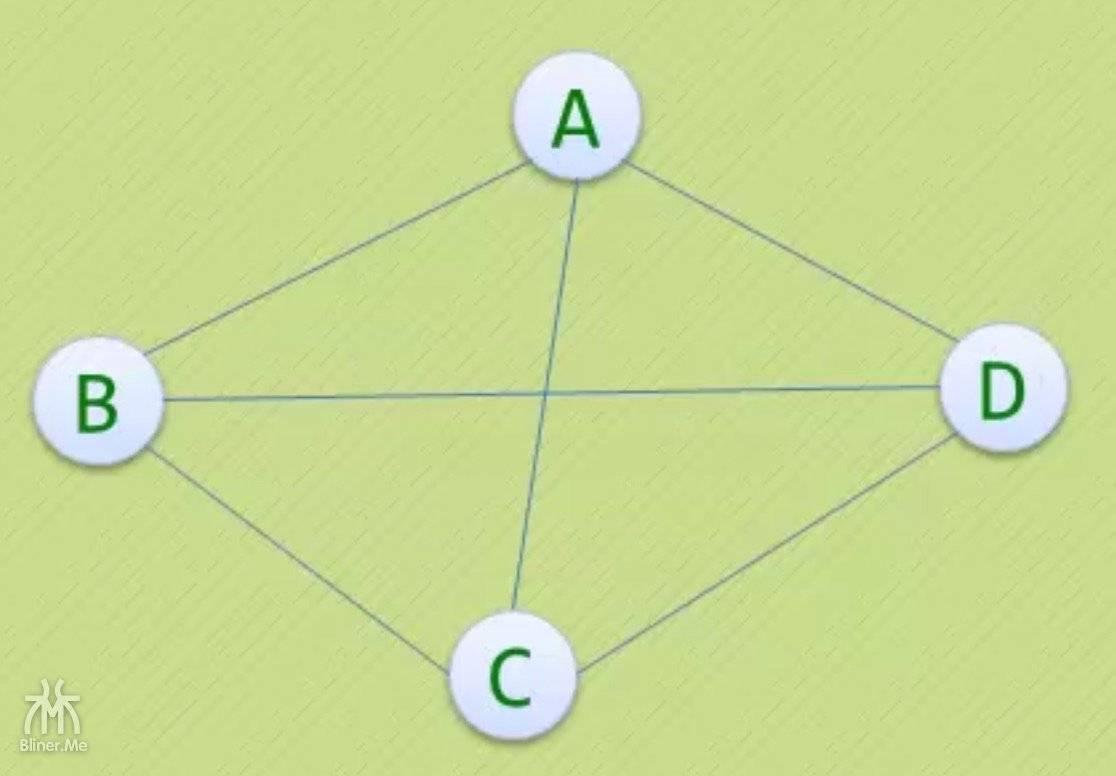
如果在一个无向图中
- 任意两个顶点之间都存在边
- 则称该图为无向完全图
- n 个顶点的无向完全图有 $n\times(n-1)\div2$ 条边
- 上面就是一张无向完全图,所有顶点都连着边
- ABCD 4个顶点就是 $4\times(4-1)\div2=6$ 条边
有向完全图

如果在一个有向图中
- 任意两个顶点之间都存在方向互为相反的两条弧
- 则称该图为有向完全图
- n 个顶点的无向完全图有 $n\times(n-1)$ 条边
- 上面就是一张无向完全图,所有顶点都与另一个顶点互为相反弧
- ABCD 4个顶点就是 $4\times(4-1)=12$ \条边
稀疏图和稠密图
这里讲的稀疏和稠密都是相对而言的,通常
- 边或者弧数小于 $n\times \log n$时的图为稀疏图
- 反之为稠密图
带权图
这里说的权根我们在哈夫曼树中说的权是一样的
- 图的边或者弧带有与它相关的数字
- 我们把这些相关树称作
权(weight) - 我们称这种
带权图为网(NetWork)
子图
如果有两个图 G1=(V1,E1)和 G2=(V2,E2)
- 如果 $V2 \subseteq V1$,G2的顶点都在 G1 的顶点的集合内
- 并且!!!
- $E2 \subseteq E1$,G2的边都在 G1 的边的集合内
- 记住,上面两个条件如果同时成立!
- 我么你就说 G2 是 G1 的子图
- 简单就是,我的顶点你也有,我的边你也有,那我就是你的子图
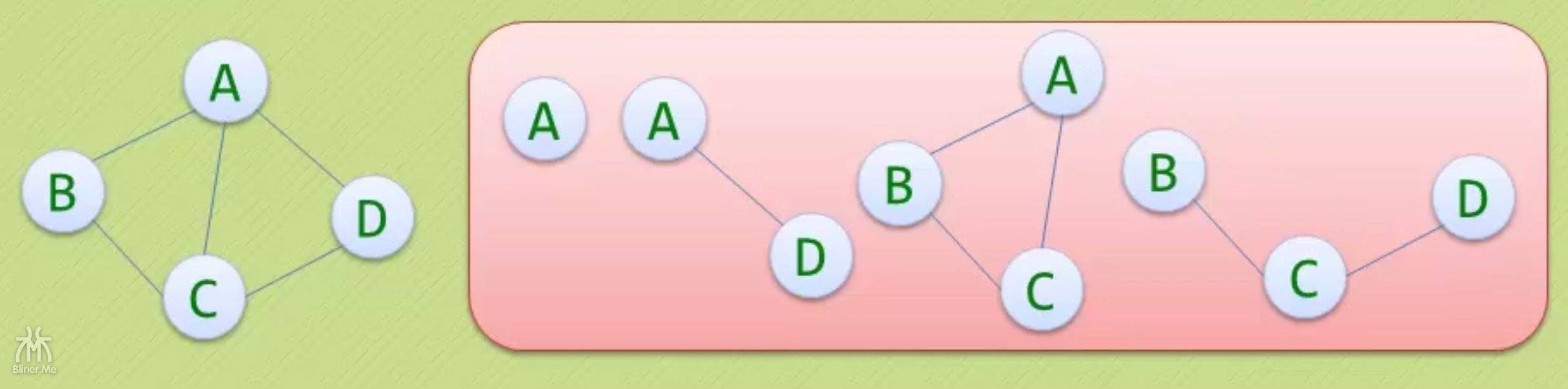
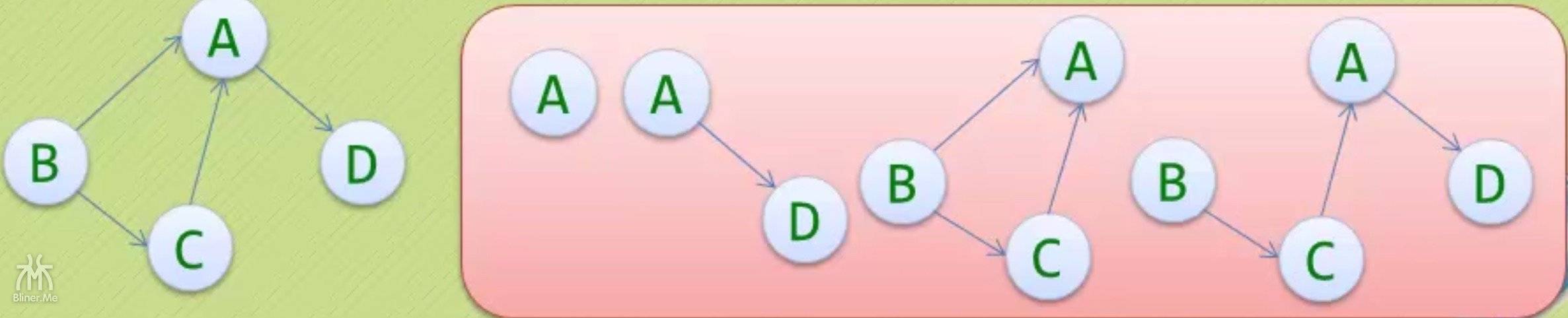
上面两张图中,红框内的都是左边图的子图。
记住有向图还要关注方向是否相同!
基础知识还有不少,我们下节继续!
尾巴
这是我的个人学习笔记,主要是应付考研复习使用,充斥着一些吐槽和个人观点,并不严谨,欢迎大家参考、指正。


