数据结构之图-图结构的简介和引入（下）-学习笔记-63

发表于 | 分类 | 评论数： | 阅读次数：

引入

前面我们基本讲了什么是图结构，以及顶点、边和弧之间不同状态的特殊图结构，我们今天继续，看看这些顶点、边和弧之间的关系。

关系

我们来讲讲顶点和边的一些关系

顶点和边的关系

我们说，如果存在一个无向图，G（V，E）

  • 图中的两个顶点构成的边$(V1 , V2)\in E$属于 E 的集合
  • 那么我们就说 V1 和 V2 互为邻接点（Adjacent）
  • 也就说明 V1 和 V2 相邻接，不是连接！。
  • 对于边(V1 , V2)来说
  • 边(V1 , V2)依附（Incident）于 顶点 V1和 V2
  • 也可以说边(V1 , V2)与顶点 V1 、V2 相关联

无向图中的度

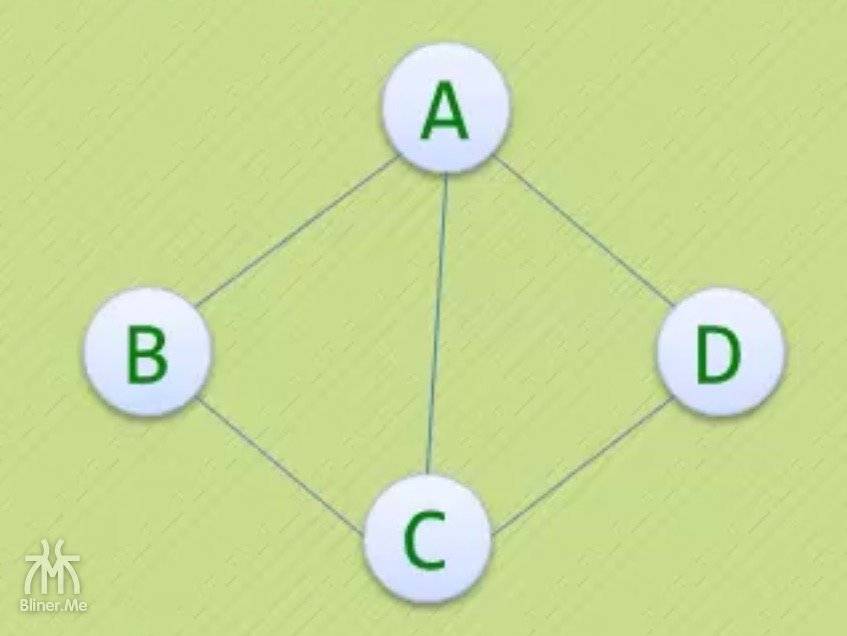
顶点 V 的度（Degree）是和 V 相关联的边的数目，记为 TD（V）

  • V 相关联得边根据上面得定义，就是根顶点 V 相连接的边
  • 上图中顶点 A、B互为邻接点
  • 边（A，B）依附于顶点 A 与 B 上
  • 顶点 A 的度为 A 关联得边得数目
  • 关联的边有（A，B）、（A，C）（A，D）
  • 所以顶点 A 得度为 3
  • B 的关联边是（B，A）、（B，C）度是 2

有向图中的度

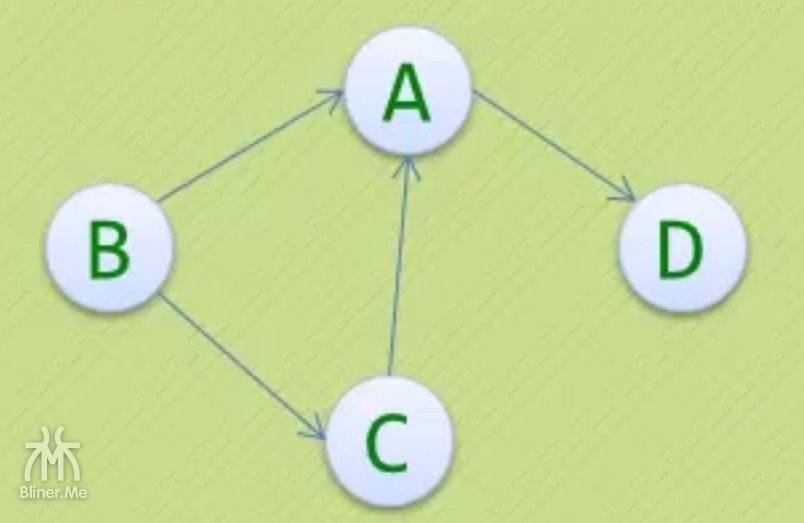
那么在有向图中的度呢？现在有有向图 G=（V，E）

  • 如果弧$<V1,V2>\in E$，注意是尖括号。属于边的集合E
  • 则称顶点 V1邻接到顶点 V2
  • 顶点 V2 邻接自顶点 V1
  • V1是弧尾，V2是弧头，所以这里得邻接是有方向的
  • 邻接自和邻接到是不同的，请注意！

所以，有向图就跟无向图不同了

  • 以顶点 V 为头的弧的数目称为 V 的入度（InDegree）记为 ID（V）
  • 以顶点 V 为尾的弧的数目称为 V 的出度（OutDegree）记为 OD（V）
  • 因此，该顶点 V 的度为$TD(V)=ID(V)+OD(V)$

我们看上面的有向图中

  • 顶点 A 为头，指向 A 的入度为2
  • 顶点 A 为尾，从 A 出去的出度为1
  • A 的度为$2+1=3$

路径

在图中，我们从一个顶点到另一个顶点的路线，称为路径（Path）

无向图的路径

以下四种是在无向图 G 中顶点 A 到顶点 D 的四种不同的路径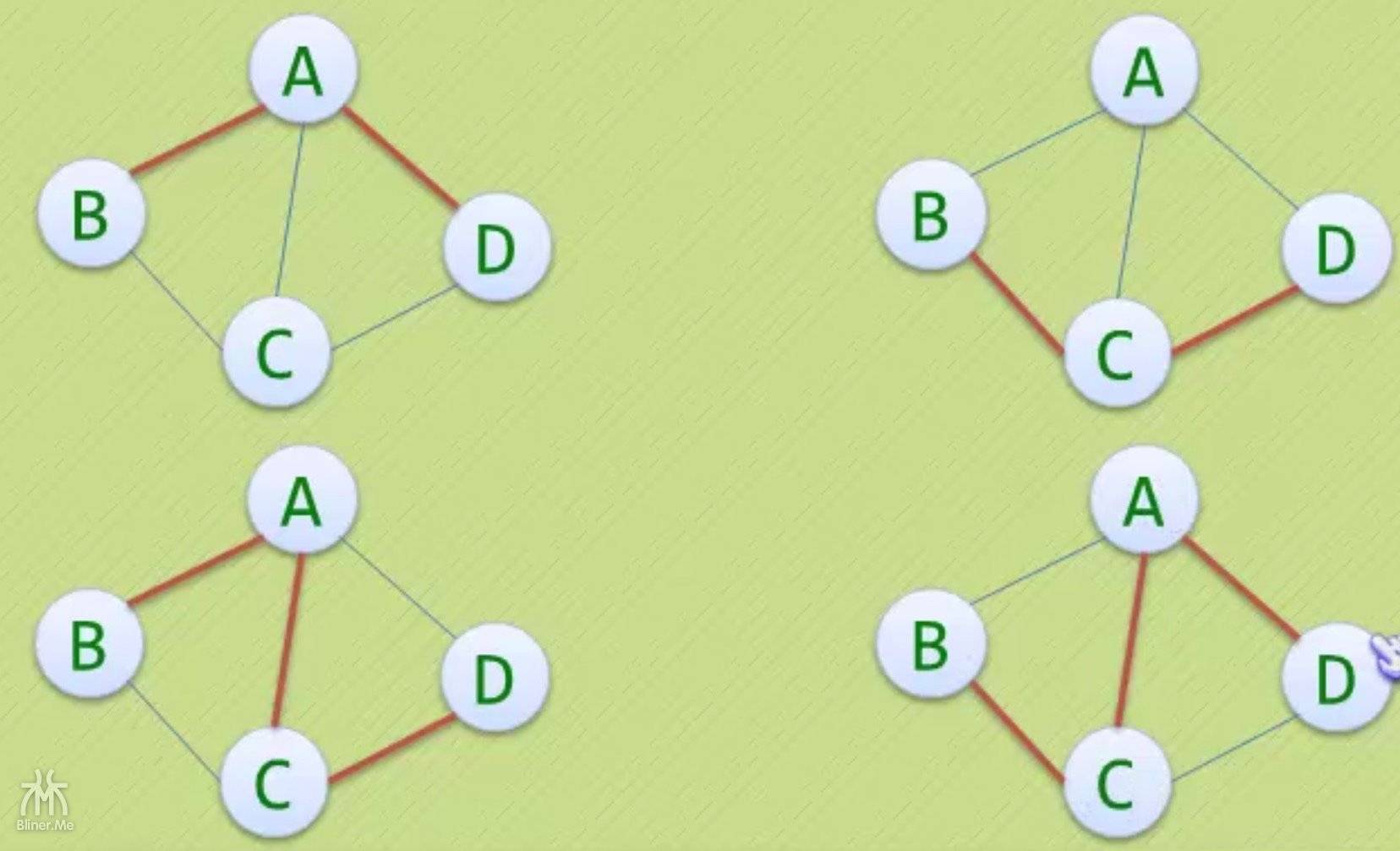

我们看到顶点到顶点之间有这么多种不同的走法

  • 以后我们学习图的主要目的就是简化路径
  • 找出最优路径

有向图的路径

以下是在有向图 G 中从 B 到 D 的路径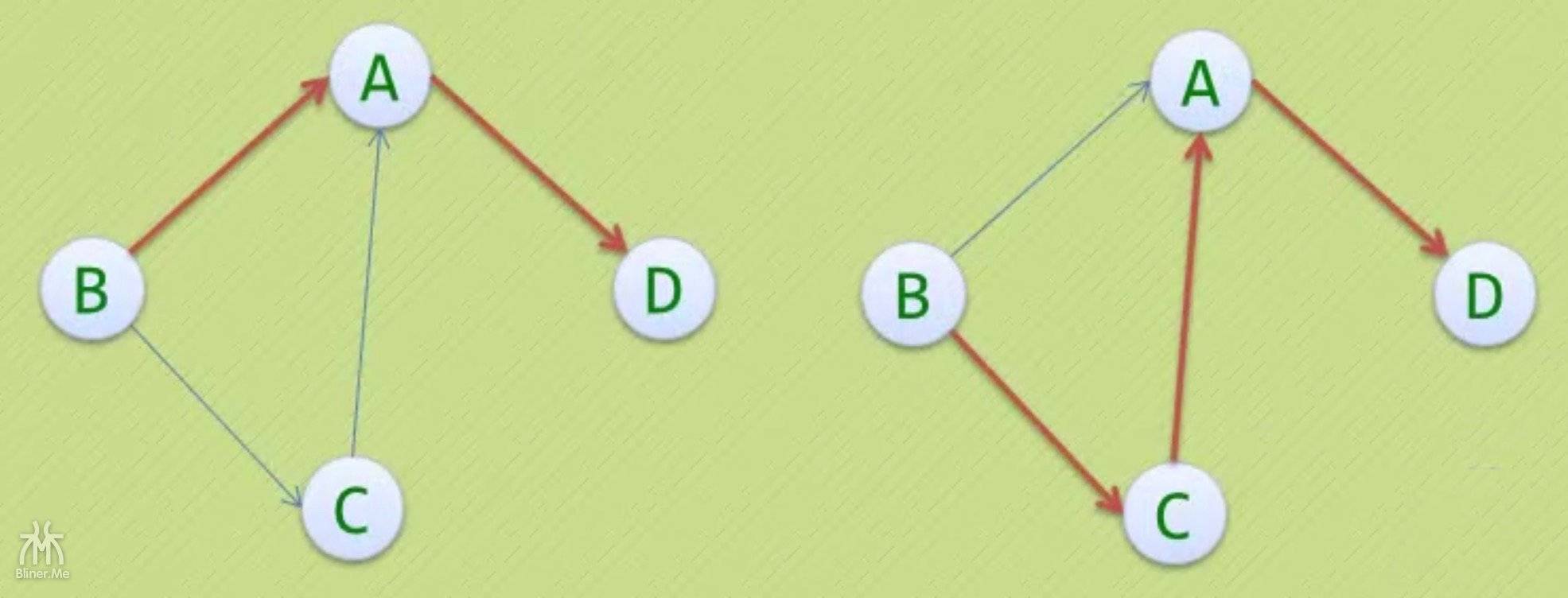

有向图的路径需要额外注意方向

  • 如果我从 A 到 B 是不行的，因为没有 A 为弧头、B 为弧尾的边。
  • 必须是按照有向图的指向来从一个顶点到另一个顶点

路径的长度

路径的长度就是路径上边或弧的数量。

回路（环）

如果从第一个顶点到最后一个顶点相同的路径，我们称之为环

简单环

既然一个顶点到最后一个顶点得路径如果相同，我们就称之为环，那么什么是简单环呢？

  • 在第一个顶点到最后一个顶点得环路上，每个顶点只出现一次。
  • 除了第一个和最后一个顶点外，其余顶点都不重复出现得回路
  • 满足以上条件，就是简单环了
  • 简单来说，就是路径上的顶点不能重复，且能构成环状。
简单环 不是简单环

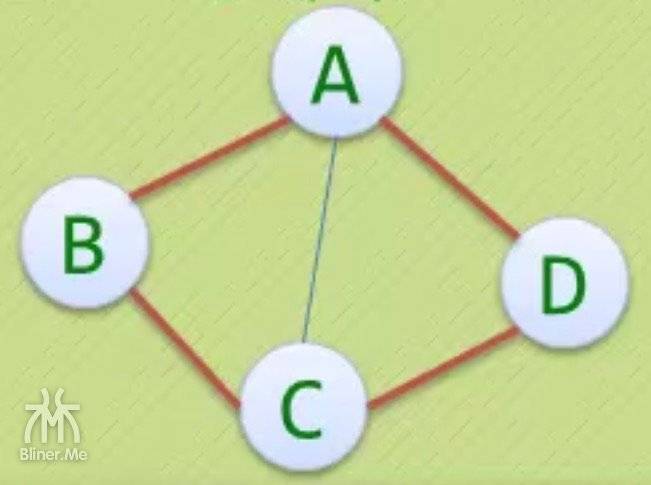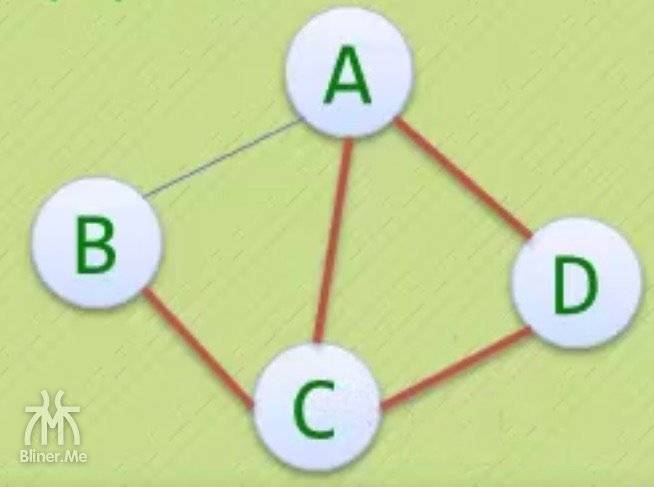右侧图不是简单环得原因是

  • 环可以是 BCADCB，C 出现了两次
  • 所以不是简单环。

连通图

如果在一个无向图中

  • 顶点 V1 到顶点 V2 有路径，则称 V1 和 V2 是连通的。
  • 如果图中得任意两个顶点 Vi 和 Vj 都是连通的
  • 我们就称这个图 G 为连通图（ConnectedGraph）
不是连通图 连通图

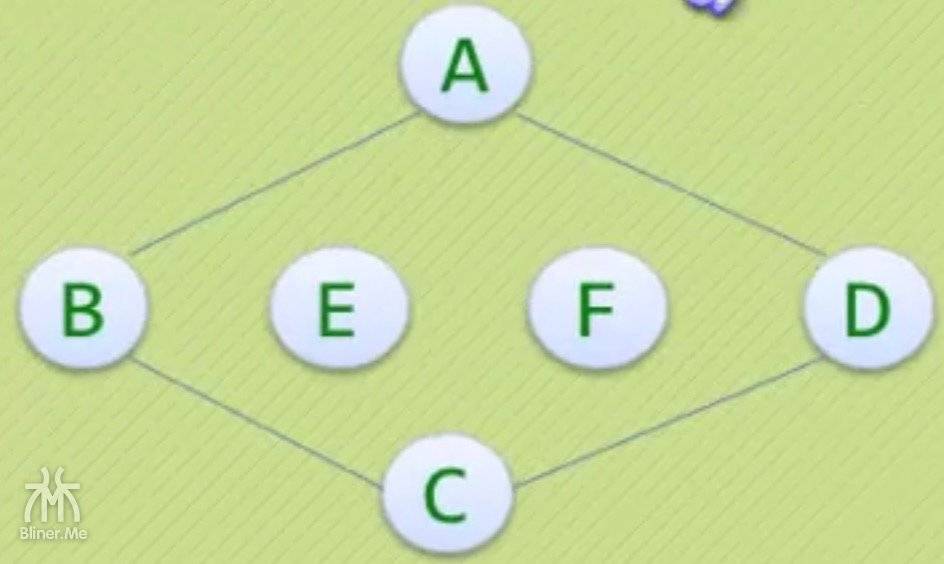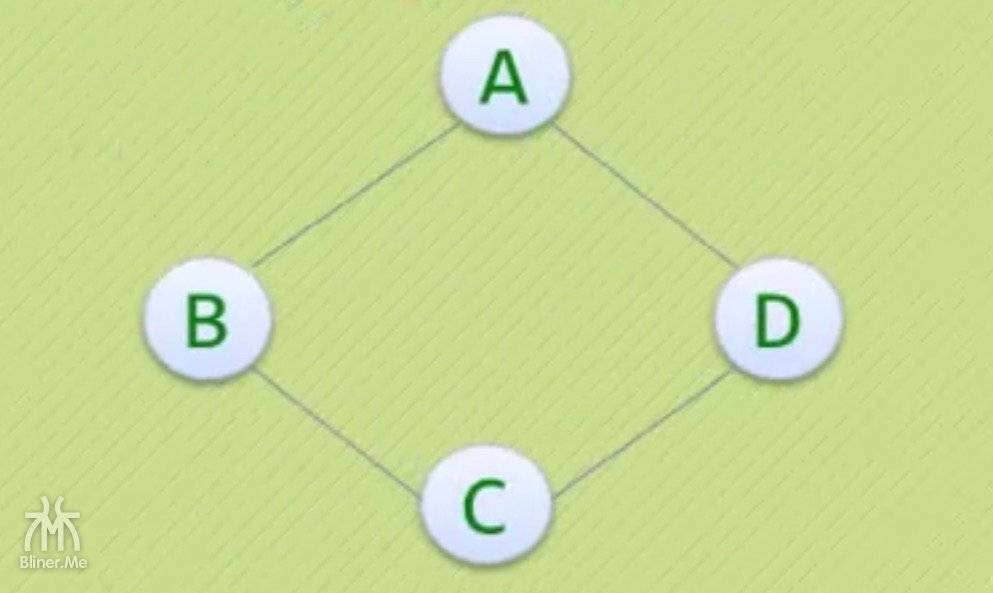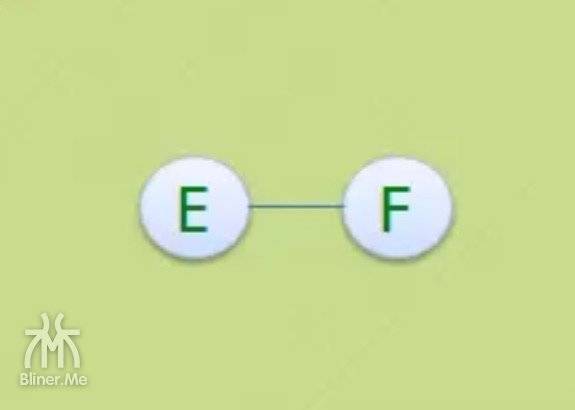
为什么左边得图不是连通图呢？因为

  • E F没有一个顶点跟 ABCD 连通
  • 所以并不是所有顶点都互相连通，不是连通图

注意：
完全图是：任意两个顶点必须是连接得，也就是得有边。
连通图是：任意两个顶点只要有路径能连过去就行。

连通分量

无向图中的极大连通子图称为连通分量。

  • 无向图，就是边没有指定方向得图。
  • 极大，就是必须包含这个子图中所有的顶点
  • 连通，就是任意两个顶点都互相连通。
  • 子图，就是顶点和边都属于无向图 G （V，E）。
  • 注意:具有极大顶点数的连通子图包含依附于这些顶点所有的边。
图 G 极大连通图-1 极大连通图-2 不是极大连通图

我们看上面的图

  • ABCD 一定是图 G 的子图
  • ABCD 的任意两个结点相互连接的
  • 子图 ABCD 顶点数也是最大
  • 那么我们就说子图 ABCD 是图 G 的极大连通子图
  • 也是图 G 的连通分量

强连通图

我们说的连通图是无向图，对于有向图来说

  • 如果对于每一对儿 Vi 到 Vj 都存在路径，则称 G 是强连通图。
  • 相应的，对于有向图中得极大强连通子图称为有向图的强连通分量。
不是强连通图 强连通图

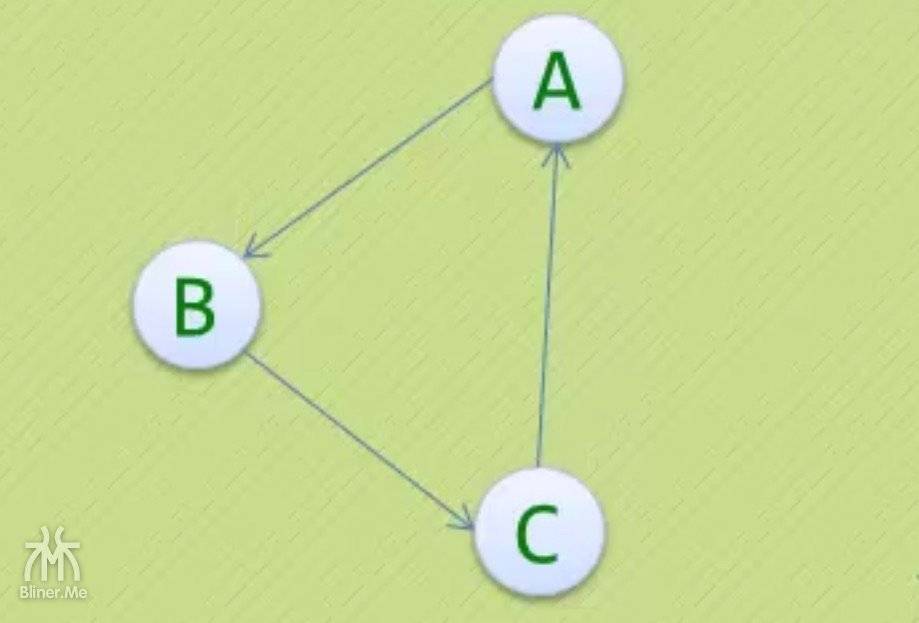为什么左侧得不是强连通图？

  • 因为任意两个顶点没有连通

但是右侧得可以是左侧图到极大强连通子图

  • 任意两个顶点联通
  • 是左侧图的子图
  • 所有的顶点都包含，极大。

连通图生成树

连通图生成树，顾名思义，通过连通图生成一棵树，连通图的生成树是一个极小的连通子图，为什么呢？因为：

  • 它含有图中全部的 n 个顶点
  • 但只有 n-1条边，因为 n-1条边就可以生成一棵树了
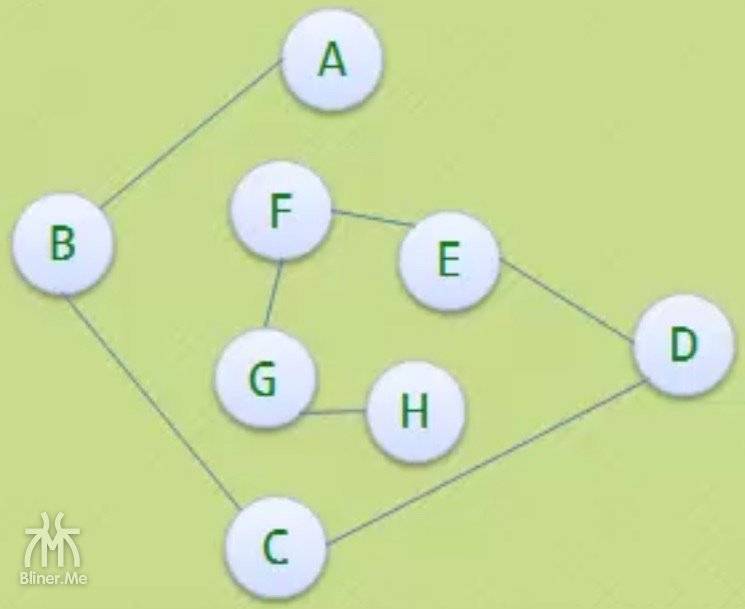
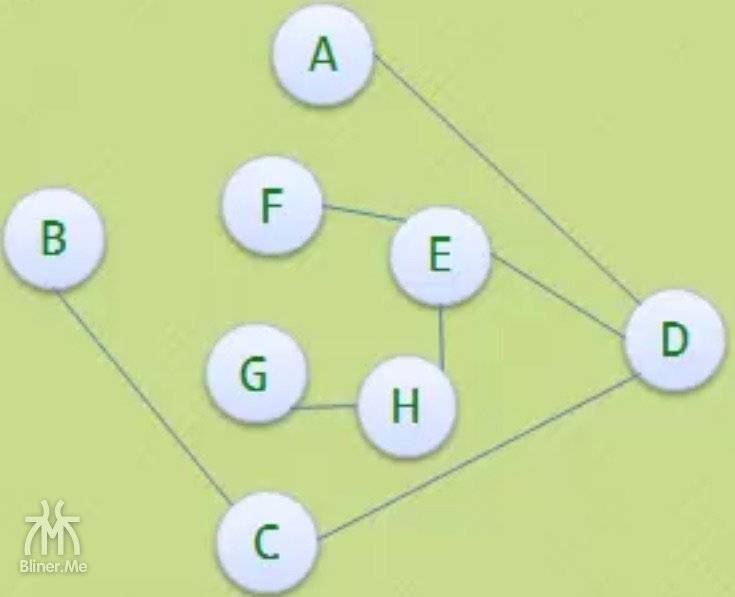
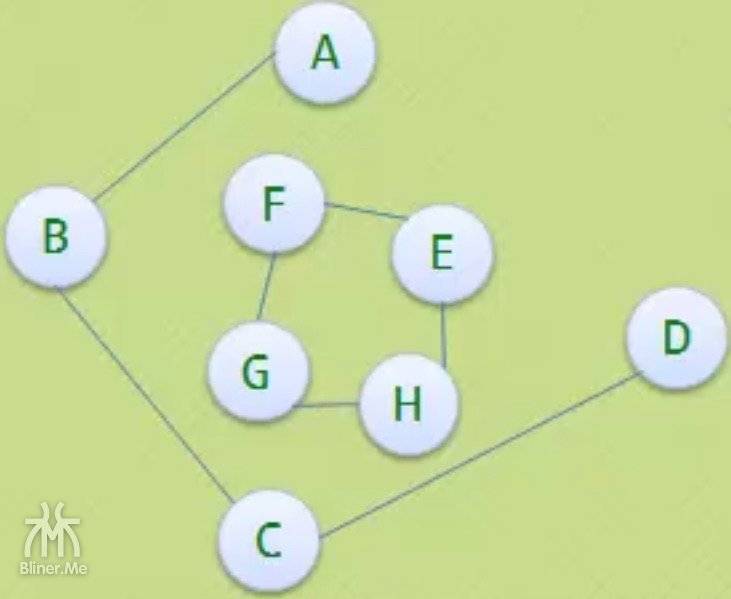
普通图 G 极小连通子图/树 极小连通子图/树 不是极小连通子图/树

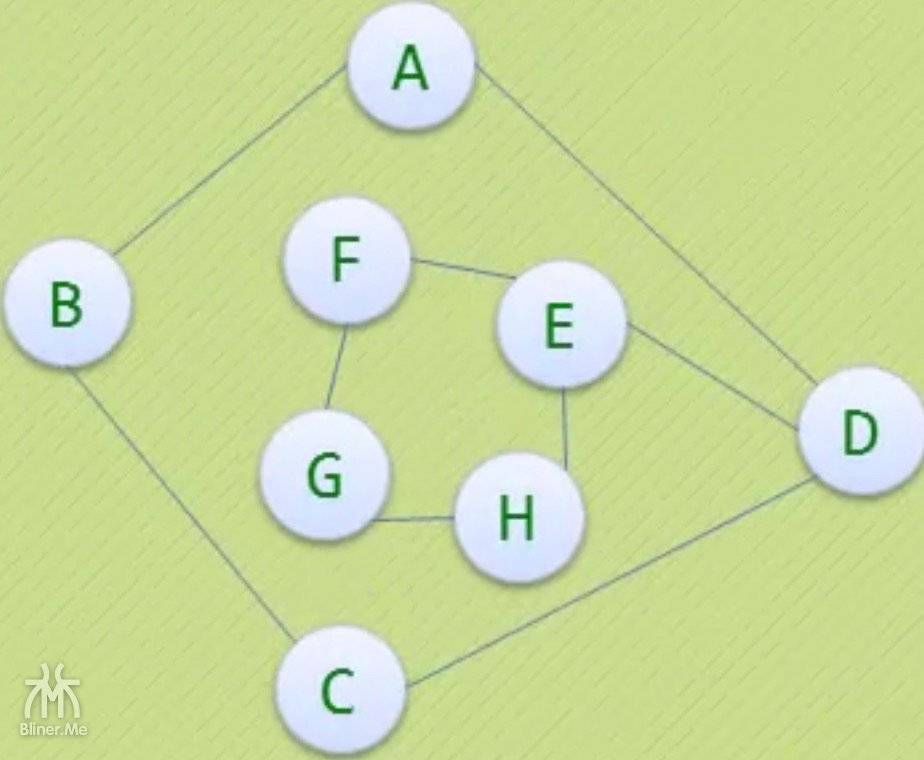
中间两个图，都符合以下条件

  • 它含有图中全部的 n 个顶点
  • 但只有 n-1条边，因为 n-1条边就可以生成一棵树了
  • 所以是极小连通子图，也是连通图生成树

最右边的图，不符合以下条件

  • 虽然符合只有 n-1 条边
  • 没有包含有图中全部的 n 个顶点
  • 所以不是极小连通子图

有向树

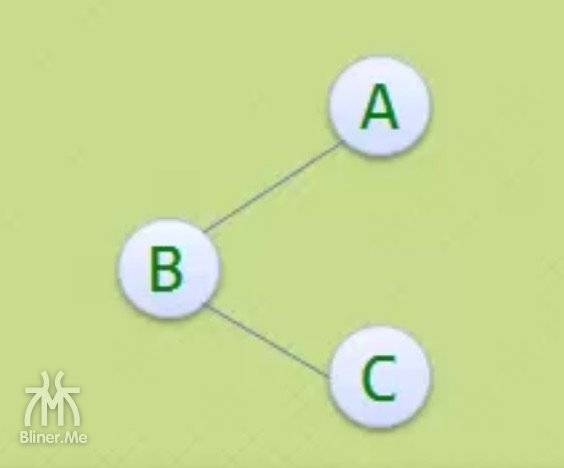
如果一个有向图，符合以下条件

  • 有一个顶点入度为0，即没有其它顶点指向它
  • 其它顶点得入度都是1，也就是其他顶点都只有一个顶点指向它
  • 我们就称这是一棵有向树。

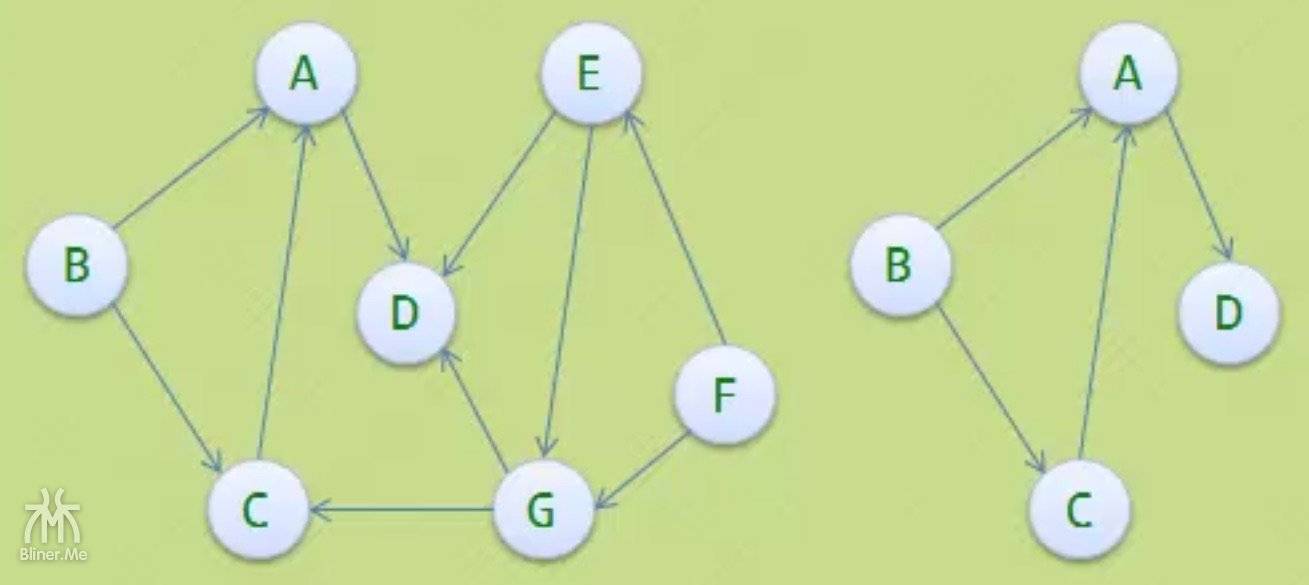
上面两张图不是有向树，左图因为 D 结点的入度为3，右图因为 A 结点入度为2

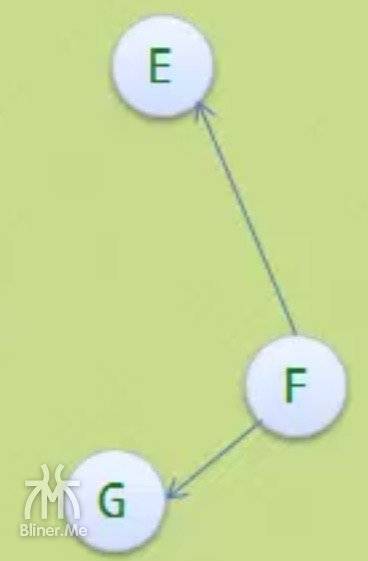
上图是有向树

  • F 得入度为0，没有顶点指向 F
  • E G的入度都为1
  • 所以上图是有向树

尾巴

这是我的个人学习笔记，主要是应付考研复习使用，充斥着一些吐槽和个人观点，并不严谨，欢迎大家参考、指正。


-------------The End-------------
你可能还喜欢
欢迎请我喝咖啡哦~！
返回首页